Publications
Early version accepted to EC (2023).
Summary. Marketplace companies rely heavily on experimentation when making changes to the design or operation of their platforms. The workhorse of experimentation is the randomized controlled trial (RCT), or A/B test, in which users are randomly assigned to treatment or control groups. However, marketplace interference causes the Stable Unit Treatment Value Assumption (SUTVA) to be violated, leading to bias in the standard RCT metric. In this work, we propose techniques for platforms to run standard RCTs and still obtain meaningful estimates despite the presence of marketplace interference. We specifically consider a generalized matching setting, in which the platform explicitly matches supply with demand via a linear programming algorithm. Our first proposal is for the platform to estimate the value of global treatment and global control via optimization. We prove that this approach is unbiased in the fluid limit. Our second proposal is to compare the average shadow price of the treatment and control groups rather than the total value accrued by each group. We prove that this technique corresponds to the correct first-order approximation (in a Taylor series sense) of the value function of interest even in a finite-size system. We then use this result to prove that, under reasonable assumptions, our estimator is less biased than the RCT estimator. At the heart of our result is the idea that it is relatively easy to model interference in matching-driven marketplaces since, in such markets, the platform mediates the spillover.
INFORMS Data Mining Section Best Paper Finalist (2021).
Abstract. Missing values are a common issue in real-world datasets.
Missing data is a common issue in real-world datasets. This paper studies the performance of impute-then-regress pipelines by contrasting theoretical and empirical evidence. We establish the asymptotic consistency of such pipelines for a broad family of imputation methods. While common sense suggests that a 'good' imputation method produces datasets that are plausible, we show, on the contrary, that, as far as prediction is concerned, crude can be good. Among others, we find that mode-impute is asymptotically sub-optimal, while mean-impute is asymptotically optimal. We then exhaustively assess the validity of these theoretical conclusions on a large corpus of synthetic, semi-real, and real datasets. While the empirical evidence we collect mostly supports our theoretical findings, it also highlights gaps between theory and practice and opportunities for future research, regarding the relevance of the MAR assumption, the complex interdependency between the imputation and regression tasks, and the need for realistic synthetic data generation models.
Abstract. Getting students to the right school at the right time can pose a challenge for school districts in the United States, which must balance educational objectives with operational ones, often on a shoestring budget. Examples of such operational challenges include deciding which students should attend, how they should travel to school, and what time classes should start. From an optimizer's perspective, these decision problems are difficult to solve in isolation, and present a formidable challenge to solve together. In this paper, we develop an optimization-based approach to three key problems in school operations: school assignment, school bus routing, and school start time selection. Our methodology is comprehensive, flexible enough to accommodate a variety of problem specifics, and relies on a tractable decomposition approach. In particular, it comprises a new algorithm for jointly scheduling school buses and selecting school start times, that leverages a simplifying assumption of fixed route arrival times, and a post-improvement heuristic to jointly optimize assignment, bus routing and scheduling. We evaluate our methodology on simulated and real data from Boston Public Schools, with the case study of a summer program for special education students. Using summer 2019 data, we find that replacing the actual student-to-school assignment with our method could lead to total cost savings of up to 8%. A simplified version of our assignment algorithm was used by the district in the summer of 2021 to analyze the cost tradeoffs between several scenarios and ultimately select and assign students to schools for the summer.
Abstract. We propose a simple model for a class of problems that we call university course scheduling problems, which encompass several related problems from the operations research literature, including course timetabling and academic curriculum planning. Our two-stage framework draws parallels between these problems and proposes a single optimization-based solving approach that can flexibly accommodate problem specifics. We applied our methods to course scheduling at MIT in the midst of unprecedented challenges and drastic capacity reductions during the COVID-19 pandemic. Our models were critical to measuring the impact of several innovative proposals, including expanding the academic calendar, teaching across multiple rooms, and rotating student attendance through the week and school year. We projected that if MIT moved from its usual two-semester calendar to a three-semester calendar, over 90% of students' courses could be satisfied on campus even with each student only on campus for two out of the three semesters. Crucially, this could be accomplished without increasing faculty workloads. For the Sloan School of Management, we also produced a new schedule which was implemented in the Fall 2020 semester. The schedule adhered to safety guidelines while allowing for half of Sloan courses to include a socially-distanced in-person component, and affording over two thirds of Sloan students the opportunity for socially distanced in-person learning in at least half their classes, despite a fourfold reduction in classroom capacity.
William Pierskalla Best Paper (2020).
Abstract. In the midst of the COVID-19 pandemic, healthcare providers and policy makers are wrestling with unprecedented challenges. How to treat COVID-19 patients with equipment shortages? How to allocate resources to combat the disease? How to plan for the next stages of the pandemic? We present a data-driven approach to tackle these challenges. We gather comprehensive data from various sources, including clinical studies, electronic medical records, and census reports. We develop algorithms to understand the disease, predict its mortality, forecast its spread, inform social distancing policies, and re-distribute critical equipment. These algorithms provide decision support tools that have been deployed on our publicly available website, and are actively used by hospitals, companies, and policy makers around the globe.
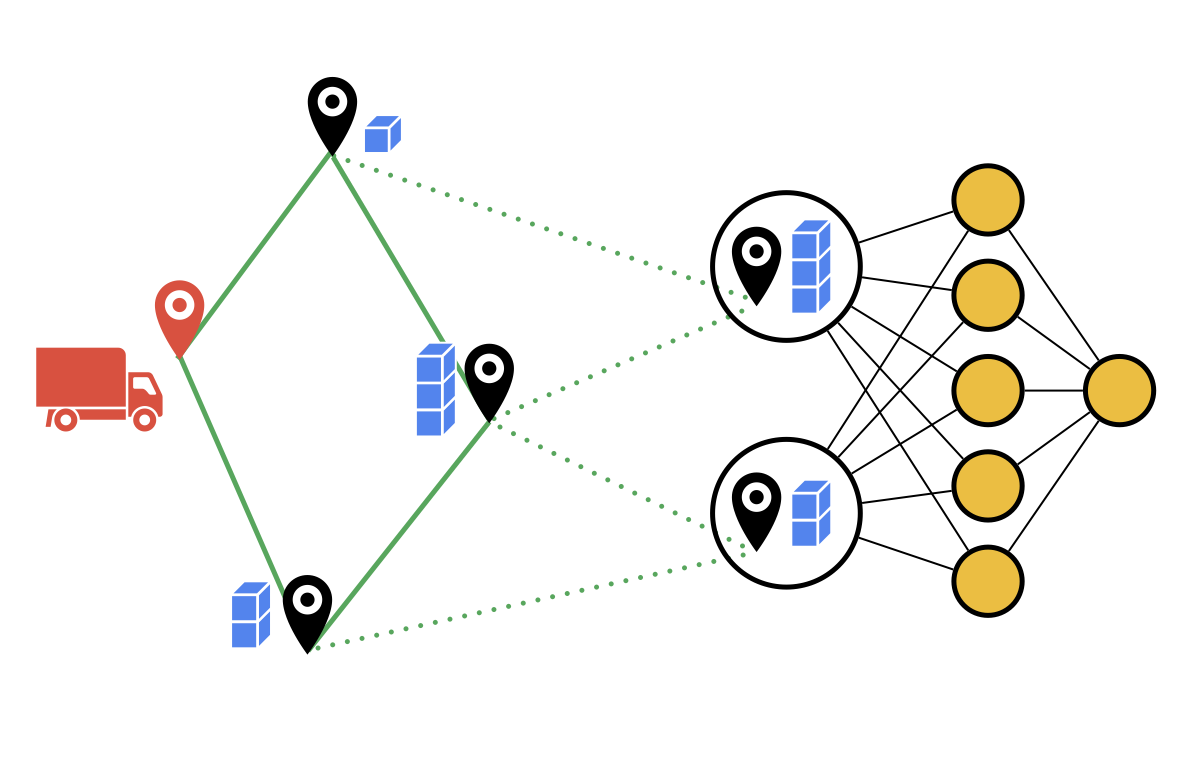
Abstract. Value-function-based methods have long played an important role in reinforcement learning. However, finding the best next action given a value function of arbitrary complexity is nontrivial when the action space is too large for enumeration. We develop a framework for value-function-based deep reinforcement learning with a combinatorial action space, in which the action selection problem is explicitly formulated as a mixed-integer optimization problem. As a motivating example, we present an application of this framework to the capacitated vehicle routing problem (CVRP), a combinatorial optimization problem in which a set of locations must be covered by a single vehicle with limited capacity. On each instance, we model an action as the construction of a single route, and consider a deterministic policy which is improved through a simple policy iteration algorithm. Our approach is competitive with other reinforcement learning methods and achieves an average gap of 1.7% with state-of-the-art OR methods on standard library instances of medium size.
Abstract. In the winter of 2016, Boston Public Schools (BPS) launched a crowdsourcing national competition to create a better way to construct bus routes to improve efficiency, deepen the ability to model policy changes, and realign school start times. The winning team came from the Massachusetts Institute of Technology (MIT). They developed an algorithm to construct school bus routes, by assigning students to stops, combining stops into routes, and optimally assigning vehicles to routes. BPS has used this algorithm for two years running; in the summer of 2017, this led to a 7% reduction in the BPS bus fleet. Bus routing optimization also gives BPS the unprecedented ability to understand the financial impact of new policies that affect transportation. In particular, the MIT research team developed a new mathematical model to select start times for all schools in the district in a way that takes transportation into account. Using this methodology, BPS proposed a solution that would have saved an additional $12M annually, and shifted students to more developmentally appropriate school start times (by reducing the number of high school students starting before 8:00 a.m. from 74% to 6% and the average number of elementary school students dismissed after 4:00 pm from 33% to 15%). However, 85% of the schools’ start times would have been changed, with a median change of one hour. This magnitude of change was too dramatic for the district to absorb, as evidenced by strong vocal opposition from some of the school communities who were negatively affected, and the plan was not implemented.
Franz Edelman Award Finalist (2019).
MIT ORC Best Student Paper (2018).
INFORMS Doing Good With Good OR Student Paper Competition Runner-up (2018).
Summary. Spreading start times allows school districts to reduce transportation costs by reusing buses between schools. However, assigning each school a time involves both estimating the impact on transportation costs and reconciling additional competing objectives. These challenges force many school districts to make myopic decisions, leading to an expensive and inequitable status quo. For instance, most American teenagers start school before 8:00 AM, despite evidence of significant associated health issues. We propose an algorithm to jointly solve the school bus routing and bell time selection problems. Our application in Boston led to $5 million in yearly savings (maintaining service quality despite a 50-bus fleet reduction) and to the unanimous approval of the first school start time reform in 30 years.
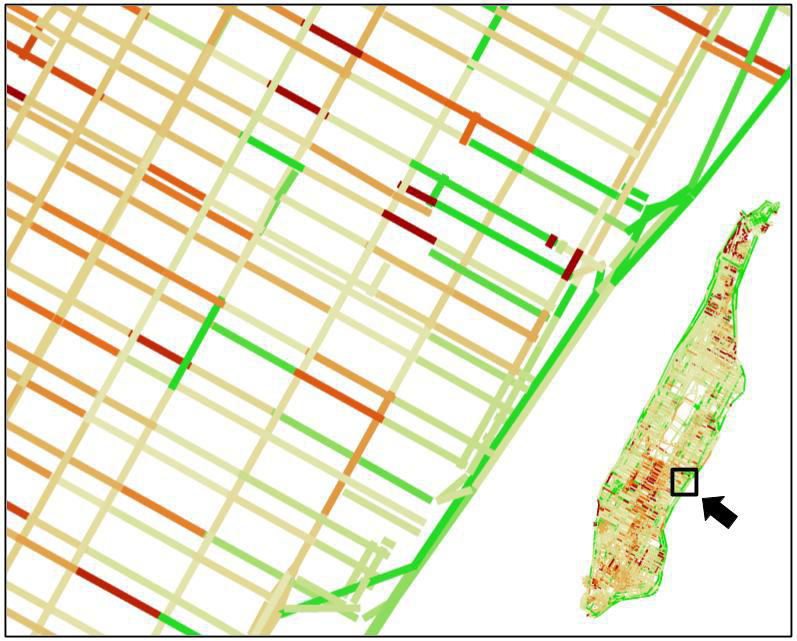
Summary. Understanding complex city traffic patterns is a major priority for modern urban planners, leading to a sharp increase in the amount and the diversity of traffic data being collected. For instance, taxi companies in many major cities now record metadata for every individual car ride, such as its origin, destination, and travel time. In this paper, we show that we can leverage network optimization insights to extract accurate travel time estimations from such origin–destination data, using information from a large number of taxi trips to reconstruct the traffic patterns in an entire city. Using synthetic data, we establish the robustness of our algorithm to high variance data, and the interpretability of its results. We then use hundreds of thousands of taxi travel time observations in Manhattan to show that our algorithm can provide insights about urban traffic patterns on different scales and accurate travel time estimations throughout the network.
